流れる空の中で数学を。

とある数学好きの「手作りすうがく」と「気ままな雑記」。

【臨界点の高精度見積もり】局在アンダーソンモデルのζ関数を近似的に試験的に構成してみた

局在 物理 臨界現象 オリジナル Python

局在アンダーソンモデル(Orthogonal class)

H=\sum_n \epsilon_n |n\gt \lt n| +\sum_{\lt n , m\gt} |n\gt \lt m|

ここで、\epsilon_nは互いに独立な確率変数で、-W/2\le \epsilon_n \le W/2の範囲で一様に分布する。\lt n , m\gtは最近接の格子点のみにわたる和を表す。

この記事では、3次元立方格子を取り扱う。

 

エネルギー準位統計

アンダーソンモデルのハミルトニアンを対角化して、エネルギーを得る。

各乱数のサンプル事に、エネルギーをE_1\lt E_2 \lt \cdots \lt E_nとしたとき、そのエネルギー準位の差を

\delta E_j=E_{j+1}-E_{j}

で計算する。ここで、\delta E_jの平均値を\delta Eとしたとき、

\epsilon_j=\delta E_j/ \delta E

とすると、この\epsilon_jのとる値の分布は局在状態で、指数分布、広がった状態で広がった分布、臨界点で系のサイズに依存しない分布が得られる。

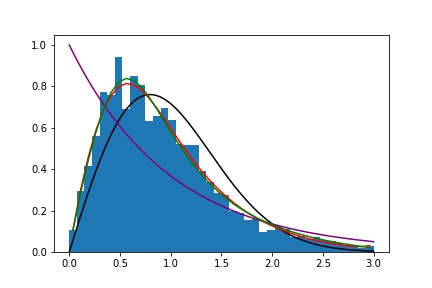
準位間隔の分布(臨界点での分布はパデ近似を使って近似関数をプロットしてある。ほかはそれぞれ、局在状態と広がった状態の分布関数である。)

臨界点での分布をパデ近似で近似した関数はW=16.338で、

p(\epsilon)=\epsilon \frac{p_0+p_1 \epsilon+p_2 \epsilon^2}{1+p_3 \epsilon + p_4 \epsilon^2 +p_5 \epsilon^3 + p_6 \epsilon^4}

[p_0,p_1,\cdots,p_6]=[2.3320977630465674, 1.9251460538218101, -0.31829353645592573, -1.4793606417094827, 12.67077149585408, -16.42315495527847, 10.545989559845134]

ζ関数とオイラー積

得られたエネルギー順位間隔の分布関数から逆に、エネルギー順位間隔を生成する。今回は200個生成した。

このような生成方法を取るので、臨界状態以外は無限系の性質をとらえられていると考えられる。

得られた順位間隔\epsilon_nに対して、

\zeta(z)=\prod_n \frac{1}{1-\epsilon_n^{-z}}

とオイラー積を定義する。本当は無限個の項をかけないと意味がないので、テイラー展開とパデ近似を使って、近似してみることにする即ち、

\zeta(z)=\prod_n \frac{1}{1-\epsilon_n^{-z}}

=\prod_n\left( 1/\ln{\epsilon_n}+\frac{1}{2}z+\frac{1}{12}\ln{\epsilon_n}z^2\right)

これを展開して、パデ近似する。今回は対角パデ近似[100/100]を用いた。

そして、得られた近似ζ関数の零点と極を調べてみた。

極は、相の状態に寄らず円形に分布することが分かった。

臨界点(W=16.338)での極

局在状態のpole

広がった状態のpole



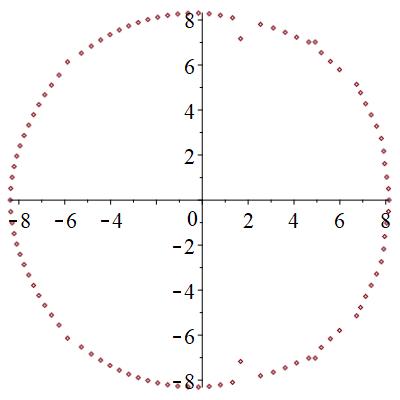
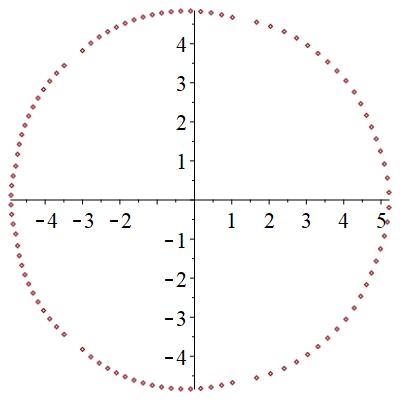
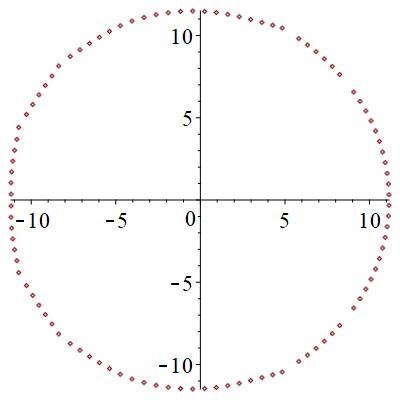
零点は、局在状態では、下図のように、広がった状態では円形に分布するものが見つかる。また、局在状態では2つの領域に分断される。臨界状態では、サンプル事に、局在か広がった状態かの２つの状態になったりならなかったりする。特に、中間的な零点分布を取ることがある。

臨界状態(W=16.338)での零点分布

広がった状態の零点分布

局在状態の零点分布

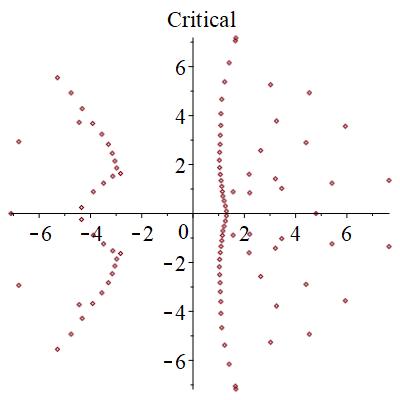
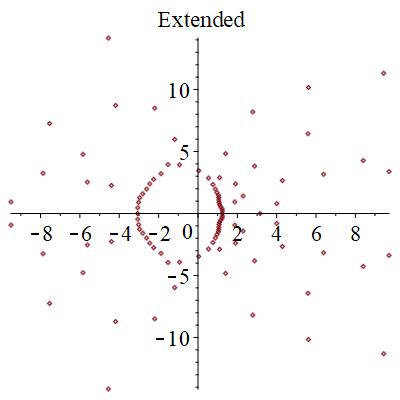
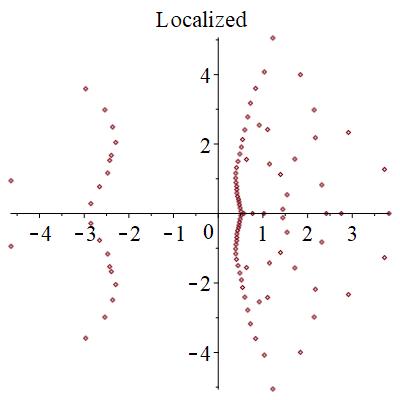
結論

零点のつながり方というトポロジカルな情報をランダムなサンプル毎に見ていくことで、臨界点がW=16.338程度であることが分かった。このように有効数字4桁～5桁程度の精度で判別できるのがこの手法の強みである。

一方で、この手法の弱みは、つながっているかどうかの判断を人の目で見て判断しているという曖昧さが残っているという点と、サンプル数が十分とれているかという問題がつきまとう点である。しかし、サンプル数をより多く取れば、臨界点のより精度の高い見積もりが可能になると考えられる。