この動画を見るとわかるが、唐突に分散が小さくなったり、平均値の位置が一瞬で飛んだりする。やはり、ほとんど不規則に見える。(うにょうにょしていてかわいい。)量子力学の確率分布の時間発展に似たなにかが現れるかもしれないと0.000001%くらい期待していたが、そんなに甘くはなかった。何か規則性のようなものを読み取れる方がいたら、ぜひ教えていただきたい。

参考までにガウス分布で平均値と標準偏差の乱数を発生させ、そこからガウス分布を再生成した場合のランダムな時間発展の動画も貼っておく。

なんだか実際のチャートの時間発展よりランダムに見える。やはり、実際のチャートは完全なランダムとはなんらかの差があるのだろうか？

一応、平均値と標準偏差の時間変化も貼っておく。

ソースコード

github.com

gistd43c90b6b030e3d5d0fb5fc9febfb8dc

まとめ

ランダム的なものは、心惹かれるなーとつくづく思う。

2022-09-26

為替レートは乱数で再現可能なのか？について

トレード為替数学 Python オリジナルプチ研究

問題提起

今も昔も為替取引が活発に行われている。しかし、その未来予測は困難とされており、実際ランダムウォークのようであるとも言われている。もし、仮に完全にランダムウォーク的であるならば、分儲けと損がそれぞれ50%の確率で起こり、手数料が引かれる分期待値は必ずマイナスとなるはずである。そこで、今回は日本円と米ドルの為替レートがランダムウォーク的かどうか検証してみることにした。

検証用元データ

検証用データは1日単位で、100日分のデータを以下のサイトから拝借した。

sec.himawari-group.co.jp

各日にちの最大値と最小値、およびその平均値をプロットすると次の図のようになる。

短期間データの標準偏差

まず各日にちについて、平均値を最大値と最小値から引き、日にちに関する平均と標準偏差を求めた。最大値と最小値で大差はなく、平均からのずれの平均が $\pm 0.744$ 程度で、標準偏差が $0.387$ 程度であった。

長期間の振る舞いがわかっている状況下での乱数によるずれ

元データの平均値から、平均値 $\pm 0.744$ 、標準偏差 $0.387$ 正規分布に従う正規分布を足したり引いたりして、少しだけ短期的な乱数の影響を入れて為替チャートを乱数を用いて再生成したのが次の図である。

この図を見る限り、実際の為替チャートと大きなずれはなく、上昇か下落かを当てる確率は約75%程度となる。

その場合の損益は手数料を２％としてもほとんどの場合黒字になる。

しかし、分布の平均的な長期の振る舞いを事前に知ることは困難なため、この例はあくまで、短期の予想に乱数が入った場合、どれほど影響が出るかを見ているに過ぎない。

長期の平均値の予想も乱数で生成してみた

5日ごとに平均値が変動するとして、正規分布で平均値０で分散が適当な(値により価格の振れ幅が変わる)乱数を生成し

長期的なふるまいをランダムウォーク的に決定し、それに短期間の乱数を加味したものをいくつか生成してみた。

黒の線が現実のチャートで、緑とピンクの線がそれぞれ、乱数によって生成されたチャートである。特に例１は実際の為替チャートと酷似しており、為替チャートがある程度ランダムになりうることを強く示唆している。上昇、下降の当たる確率はおよそ１/2で、期待値はマイナスになる傾向が大きかった。

疑問

いくら乱数で生み出されたチャートが現実のチャートと酷似しているとはいえ、為替の取引を行っているのは人間もしくはアルゴリズムに従ったコンピューターである。そこには、なんらかの意思や傾向が含まれているはずであるのに、なぜ乱数で生成したチャートが実際のチャートと酷似してしまうのか疑問である。ひょっとすると、僕たちの目の錯覚や思い込みで実際により詳細にデータを分析すれば、乱数が生成したチャートと現実のチャートの違いを判定する方法が存在するのかもしれないが今のところ不明である。

一人ひとり異なるとはいえ、戦略をもって行われているはずの、大衆の意思決定の結果がランダムになりうるのか？この疑問を解決するには実際のチャートとランダムなチャートをより詳細に調べる数学的ツールが必要になってくると思われる。

プログラム

今回、検証に用いたプログラムを貼っておく。

github.com

gistf372e9769e151f617285828c3f8caed6

2022-09-03

局在アンダーソンモデルの臨界点の次元依存性( dimensional dependence of the critical point of the Anderson model with box distribution )の線形フィット

プチ研究物理局在

局在アンダーソンモデルの臨界点の次元依存性(dimensional dependence of the critical point of the Anderson model with box distribution)

局在アンダーソンモデルでbox distributionを仮定したときの臨界点が整数次元についてほぼ線形に増加していることに気づいたので、フィッティングの結果をここにメモしておく。僕の先行研究とGarcia-Garciaさんたちの結果を線形フィットしてみた結果が次の図である。

式は、

$W_c=-42.7184 + 19.6572d$

である。 $d=2$ で[W_c=0]となるようにフィッティングし直すと、

で式は、

$W_c \simeq 18.523(d - 2)$

である。

本来であれば、僕の過去研究(https://journals.jps.jp/doi/abs/10.7566/JPSJ.83.084711)に載せるべき結果であったが、先行研究の6次元のデータをうっかり見落としていて、線形でないように見えていたのが問題であった。

2022-09-01

級数の極限値と総和法の関係について

2点総和法多点総和法数学プチ研究

指数関数とパデ近似と極限

指数関数の級数展開で $x \rightarrow \infty$ の極限を考えてみよう。

$exp(x)=\sum_{n=0}^{\infty}\frac{x^n}{n!}$ ……①

パデ近似を用いて、関数列を生成すると、

$[0/1],[1/2],[2/3],\cdots$ ……②

$[0/0],[1/1],[2/2],\cdots$ ……③

$[1/0],[2/1],[3/2],\cdots$ ……④

などが考えらえる。ところが、①式の右辺の極限値を先にとると、級数の次数の増加に関係なく、②の場合は、 $z\rightarrow \infty$ で明らかに０に収束し、④の場合は、 $z\rightarrow \infty$ では明らかに正の無限だいに発散する。

このように、級数の極限値をとるとき、どのような総和法を選択するかによって、値が変わってくるのだ。ちなみに、

$lim_{x\rightarrow \infty} abs([n/n]) =lim_{x\rightarrow \infty}|(-1)^n|=1$

となる。言いたいことは、指数関数という無限遠で明らかに発散しそうな関数でさえ、総和法の取り方次第で、極限値がかわってしまうのだ。それどころか多点総和法を用いれば、任意の値に収束させることができてしまう。

僕の今日書いた記事で、

sky-time-math.hatenablog.jp

総和法を問題点として提起して留まっているのもここに根本的な理由がある。級数と総和法の「自然な関係」とは一体なんなのだろうか？

2022-09-01

SRWS理論を用いて、臨界指数を計算するための新しい道筋(未完)

オリジナル局在研究臨界現象数学

SRWS理論におけるグリーン関数の級数展開(t>lを仮定)

部分積分を用いれば、二項係数の和の問題をある程度回避できると気づいたのでメモ。

なお、viXraにあげてあるプレプリントで使っていた無限次元近似は、使っても使わなくても厳密に計算した場合と同じ結果を与えることがわかったので報告しておく。

この記事で紹介する方法は、プレプリントのマイナーアップデートである。

グリーン関数の級数展開は次の式で与えられる。

$G(|x-y|,z) \simeq z^{|x-y|+1} \sum_{n=0}^{\infty} c_n z^n$

$A_xy=k^t t^{-d/2}$

$c_n =\sum_{t=|x-y|}^{|x-y|+n}A_{xy}(t)\left(\frac{2}{W}\right)^{t+1}\binom{n+|x-y|}{t}$

積分近似と部分積分

総和公式を積分と合わせて近似する。

$\sum_{t=|x-y|}^{|x-y|+n} (2k/W)^t\binom{n+|x-y|}{t}\simeq\sum_{t=0}^{|x-y|+n} (2k/W)^t\binom{n+|x-y|}{t}=(2k/W)^{n+|x-y|}$

これを積分で近似して、

$\int_{t=|x-y|}^{|x-y|+n} (2k/W)^t\binom{n+|x-y|}{t}\simeq (2k/W)^{n+|x-y|}$

となる。部分積分を用いて、

$c_n\simeq\frac{1}{W} \int_{t=|x-y|}^{|x-y|+n}t^{-d/2}\left( \frac{2k}{W} \right)^t \binom{n+|x-y|}{t}$

$=\left[ t^{-d/2}(2k/W)^t\right]_{t=|x-y|}^{t=n+|x-y|}+(d/2)\int_{t=|x-y|}^{|x-y|+n}t^{-d/2}\left( \frac{2k}{W} \right)^t$

$\simeq\left[ t^{-d/2}(2k/W)^t\right]_{t=|x-y|}^{t=n+|x-y|}+(d/2)\sum_{t=|x-y|}^{|x-y|+n}t^{-d/2}\left( \frac{2k}{W} \right)^t$

nに依存する項だけを残すと、

$c_n\simeq \frac{1}{W} [(n+|x-y|)^{-d/2}a^{n+|x-y|}]+(d/2)\Phi(a,d/2+1,n+|x-y|+1)$

$c_n\simeq \frac{1}{2k}a [(n+|x-y|)^{-d/2}a^{n+|x-y|}]+(d/2)\Phi(a,d/2+1,n+|x-y|+1)$

ここで、Φはレルヒの超越関数であり、

$a=\frac{2k}{W}$

次に $n$ に関する和

$G(|x-y|,z) \simeq z^{|x-y|+1} \sum_{n=0}^{\infty} c_n z^n$

を、 $G(|x-y|,z)\propto z (z\rightarrow \infty)$ となるように総和を取らないといけないが方法は今のところ不明である。

$c_n$ の第一項については、

$G_1(|x-y|,z) \equiv z^{|x-y|+1} \sum_{n=0}^{\infty} \frac{1}{2k}a [(n+|x-y|)^{-d/2}a^{n+|x-y|}\ z^n$

$G(|x-y|,z) \propto za \sum_{n=0}^{\infty} (n+|x-y|)^{-d/2}(az)^{n+|x-y|}$

$G(|x-y|,z) \equiv za f_1(az)$

$G(|x-y|,z) \propto za$

なので、第一項は無視してよいことが分かる。

追記(2022/09/02):少し進展があった。詳細は以下の記事で。

sky-time-math.hatenablog.jp

2022-08-18

2次方程式の複素数解とグラフの幾何学的関係

数学高校数学

2次関数と2次方程式

2次関数

$y=ax^2+bx+c$

と2次方程式

$ax^2+bx+c=0$

を考える。2次方程式が実数解を持つとき、その解は、 $y=ax^2+bx+c$ と $y=0$ の交点で与えられる。

それでは、複素数解を持つときはどうなるだろうか？

幾何学的に考察してみよう。

2次方程式の解の公式

2次方程式が実数解を持たないと仮定すると、

$x=\frac{-b\pm \sqrt{4ac-b^2} i }{2a}$

一方 $y=ax^2+bx+c$ のグラフの頂点は、

$y=a\left(x+\frac{b}{2a}\right)bx+\frac{4ac-b^2}{4a}$

より、 $\left(-\frac{b}{2a}, \frac{4ac-b^2}{4a} \right)$

となる。

さて、このようにして得られたグラフの頂点を、元のグラフの頂点と比べる。すると、ｘ座標は同じで、ｙ座標はいくらかずれている。そして、そのｘ座標は2次方程式の複素数解の実部に等しく、ｙ座標は2次方程式複素数解の虚部の定数倍に等しい。

このようにして、2次方程式の複素数解と元のグラフとの関係が得られた。

実数解の場合グラフの軸から等距離にｘ軸方向に等距離にずれた位置の点に解があった。複素数解の場合、グラフの頂点からy軸方向にｘ軸から上下に等距離ずれた位置の点に対応する解がある。

このように実数解の場合も複素数解の場合も、ｘ軸上のある点から等距離ずれた場所に２つの解に対応する点があることが分かった。

2022-07-17

【臨界点の高精度見積もり】局在アンダーソンモデルのζ関数を近似的に試験的に構成してみた

局在物理臨界現象オリジナル Python

局在アンダーソンモデル(Orthogonal class)

$H=\sum_n \epsilon_n |n\gt \lt n| +\sum_{\lt n , m\gt} |n\gt \lt m|$

ここで、 $\epsilon_n$ は互いに独立な確率変数で、 $-W/2\le \epsilon_n \le W/2$ の範囲で一様に分布する。 $\lt n , m\gt$ は最近接の格子点のみにわたる和を表す。

この記事では、 $3$ 次元立方格子を取り扱う。

エネルギー準位統計

アンダーソンモデルのハミルトニアンを対角化して、エネルギーを得る。

各乱数のサンプル事に、エネルギーを $E_1\lt E_2 \lt \cdots \lt E_n$ としたとき、そのエネルギー準位の差を

$\delta E_j=E_{j+1}-E_{j}$

で計算する。ここで、 $\delta E_j$ の平均値を $\delta E$ としたとき、

$\epsilon_j=\delta E_j/ \delta E$

とすると、この $\epsilon_j$ のとる値の分布は局在状態で、指数分布、広がった状態で広がった分布、臨界点で系のサイズに依存しない分布が得られる。

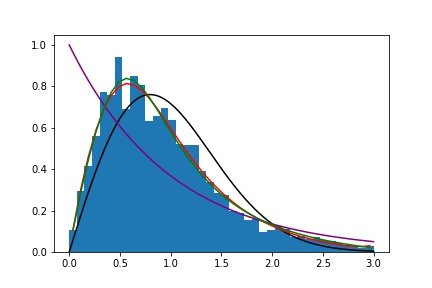
準位間隔の分布(臨界点での分布はパデ近似を使って近似関数をプロットしてある。ほかはそれぞれ、局在状態と広がった状態の分布関数である。)

臨界点での分布をパデ近似で近似した関数は $W=16.338$ で、

$p(\epsilon)=\epsilon \frac{p_0+p_1 \epsilon+p_2 \epsilon^2}{1+p_3 \epsilon + p_4 \epsilon^2 +p_5 \epsilon^3 + p_6 \epsilon^4}$

$[p_0,p_1,\cdots,p_6]=[2.3320977630465674, 1.9251460538218101, -0.31829353645592573, -1.4793606417094827, 12.67077149585408, -16.42315495527847, 10.545989559845134]$

ζ関数とオイラー積

得られたエネルギー順位間隔の分布関数から逆に、エネルギー順位間隔を生成する。今回は200個生成した。

このような生成方法を取るので、臨界状態以外は無限系の性質をとらえられていると考えられる。

得られた順位間隔 $\epsilon_n$ に対して、

$\zeta(z)=\prod_n \frac{1}{1-\epsilon_n^{-z}}$

とオイラー積を定義する。本当は無限個の項をかけないと意味がないので、テイラー展開とパデ近似を使って、近似してみることにする即ち、

$\zeta(z)=\prod_n \frac{1}{1-\epsilon_n^{-z}}$

$=\prod_n\left( 1/\ln{\epsilon_n}+\frac{1}{2}z+\frac{1}{12}\ln{\epsilon_n}z^2\right)$

これを展開して、パデ近似する。今回は対角パデ近似 $[100/100]$ を用いた。

そして、得られた近似ζ関数の零点と極を調べてみた。

極は、相の状態に寄らず円形に分布することが分かった。

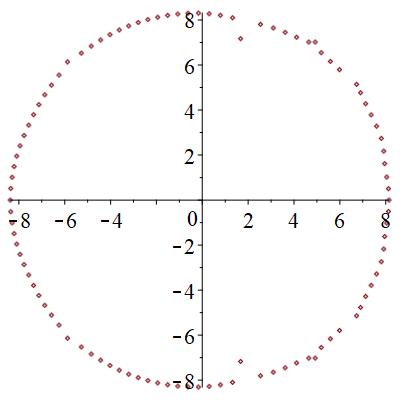
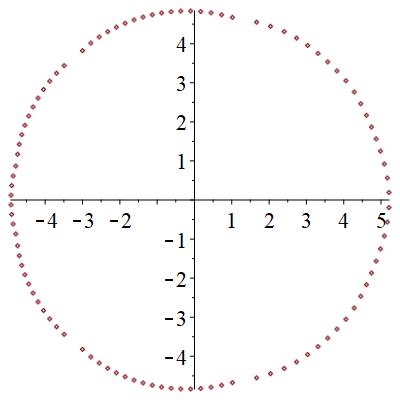
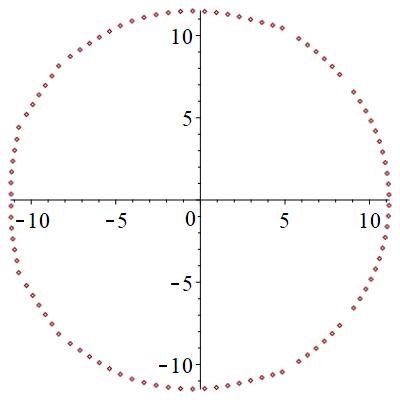
零点は、局在状態では、下図のように、広がった状態では円形に分布するものが見つかる。また、局在状態では2つの領域に分断される。臨界状態では、サンプル事に、局在か広がった状態かの２つの状態になったりならなかったりする。特に、中間的な零点分布を取ることがある。

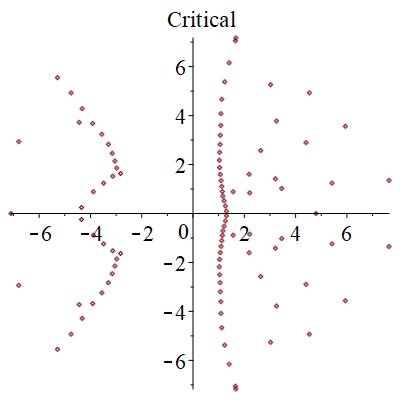
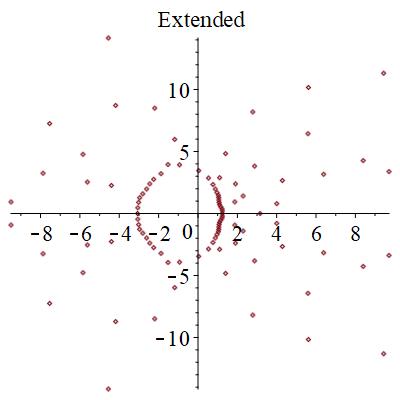
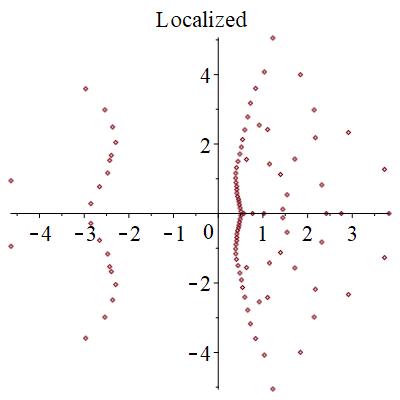
結論

零点のつながり方というトポロジカルな情報をランダムなサンプル毎に見ていくことで、臨界点が $W=16.338$ 程度であることが分かった。このように有効数字4桁～5桁程度の精度で判別できるのがこの手法の強みである。

一方で、この手法の弱みは、つながっているかどうかの判断を人の目で見て判断しているという曖昧さが残っているという点と、サンプル数が十分とれているかという問題がつきまとう点である。しかし、サンプル数をより多く取れば、臨界点のより精度の高い見積もりが可能になると考えられる。

流れる空の中で数学を。

とある数学好きの「手作りすうがく」と「気ままな雑記」。

為替トレードの不規則な動きを可視化してみた

前回のランダムな結果を受けて

トレードのデータ

一定時間でサンプリングして統計を取る