流れる空の中で数学を。

とある数学好きの「手作りすうがく」と「気ままな雑記」。

1994トルコ数学オリンピックを解いてみた

twitter 数学 数学オリンピック 整数問題bot②

数学関連の絶版本・品切れ本をコチラから購入できます！

1994トルコ数学オリンピック

最近twitterで「おはようございます。」すると、すぐ近くで「全て求めよ」って返ってくる呪いにかかったらしいFoxQです。というわけで今日のお題は、次の問題です。

 

 意外と簡単だった。

解答

２次方程式とみなして解く。

t^2+1=s(s+1)……(1)

のままだと、埒が明かないので、式変形して、

s^2+s-t^2-1=0

とする。これをsに関する2次方程式と見て、判別式をDとすると、

D=4t^2+5

となる。sが整数となるためには判別式が平方数r^2*1でなければいけないので、

4t^2+5=r^2

とおける。これを変形して、

5=(r-2t)(r+2t)

tが正の整数であることに注意すると*2、

r-2t=1
r+2t=5

となる。これを解いて、

(r,t)=(3,1)

これを(1)式に代入して解くと、

(s,t)=(1,1)

のみが解であることがわかる。

*1:rは整数

*2:もう一方の組み合わせは、(r,t)=(3,-1)となり不適

2013インド数学オリンピックを解いてみた

数学 数学オリンピック twitter 追記あり、一部未完成 整数問題bot②

数学関連の絶版本・品切れ本をコチラから購入できます！

追記(2019/08/24):(10)式の第1因子からs=0としたところに、証明の飛躍があったので修正しました。

2013インド数学オリンピック

今日はtwitterで見かけた以下の問題を解いていた。

因数分解と場合分け

まずは、因数分解していく作戦をとる。

m(4m^2+m+12)=3(p^n-1)
\Rightarrow 4m^3+m^2+12m+3=3p^n

これを強引に因数分解すると、

(4m+1)(m^2+3)=3p^n……(1)

となる。4m+1が3で割り切れる場合と、m^2+3が3で割り切れる場合に場合分けする。

①4m+1が3で割り切れる場合

法を3として、

 4m+1 \equiv m+1 \equiv 0

よって、

m=3k-1 \; (k \ge 1)

と書ける。このとき、(1)式より、4m+1を3で割って、

p^n=(4k-1)(9k^2-6k+4)

を得る。よって、l(\le n)を正の整数として、

4k-1=p^l……(2)
9k^2-6k+4=p^{n-l}……(3)

と書ける。pは5以上の素数なので、

l \ge 1
n-l \ge 1

である。(2)式より、

4k=p^l+1

これを(3)式に16をかけたものに代入して、

9(p^l-1)-24(p^l+1)+4=p^{n-l}
-p^{n-l}+9p^{2l}-6p^l=11……(4)

そこで、pを法とすると、l \ge 1とn-l \ge 1に注意して、

0 \equiv 11 \; (\bmod p)

これを満たす素数pは、11のみである。
ところで、(4)式に戻って法を5にとると

p=11 \equiv 1

なので、

-1-1-1\equiv 1
\Rightarrow 2\equiv 1

となり、矛盾である。よって、4m+1は3で割り切れない。

②m^2+3が3で割り切れる場合

 m^2 \equiv 0 \; (\bmod 3)

これは、mが3の倍数であることを意味するので、

m=3k

とおく。(1)式に戻って、3で割ると、

p^n=(12k+1)(3k^2+1)……(5)

を得る。よって、l(\le n)を正の整数として、

12k+1=p^l……(6)
3k^2+1=p^{n-l}……(7)

と書ける。pは5以上の素数なので、

l \ge 1
n-l \ge 1

である。また、

12k=p^l-1

なので、(7)式に48(=12 \times 4)をかけて、代入すると、

(p^l-1)^2+48=48p^{n-l}
\Rightarrow p^{2l}-2p^l+49=48p^{n-l}
\Rightarrow 49=48p^{n-l}-p^{2l}+2p^l

ここで、pを法とすると、 l \ge 1とn-l \ge 1に注意して、

49=7^2 \equiv 0 (\bmod p)

を得る。これを満たす素数は

p=7

のみである。(6)式より、

12k+1 \equiv 0 \; (\bmod 7)
\Rightarrow 5k \equiv 6 (\bmod 7)

gcd(5,7)=1なので、この方程式の解は7を法としてただ１つだけ存在する。その値は、

k \equiv 4 \; (\bmod 7) 

よって、sを正の整数として、

k=7s+4……(8)

と表せる。したがって、

m=3(7s+4)=21s+12……(9)

である。(5)式に(8)式を代入すると、

(21s+49)(3(7s+4)^2+1)=7^n
(21s+49)(147s^2+168s+49)=7^n……(10)

ここで、第１因子が7の冪乗になるためには、

(21s+49)=7(3s+7)

なので、u \ge 0を正の整数として、第1因子が7^{u+2}になったとすると

s=7 \times \frac{7^u-1}{3}……(11)

となる。これを(10)式の第2因子に代入すると、第2因子は、

49(7(7^u-1)+8(7^u-1)+1)
49(7^{u+1}+8\times 7^u-14)

これはu\ge1のとき明らかに7の冪乗にならない。よって、u=0で、(11)式より

s=0

となる。このとき、(9)式より、

m=12

また、(10)式より、

n=4

となる。

解答

よって、求める解は、

p=7,m=12,n=4

である。

【twitter】ウクライナ数学オリンピック2009を解いてみた【数学オリンピック】

twitter 数学 数学オリンピック 整数問題bot②

数学関連の絶版本・品切れ本をコチラから購入できます！

ウクライナ数学オリンピック2009

twitterで見かけた問題を解いてみた。よくある「～を満たすものを全て求めよ。」系の次の問題である。

解答(序盤)

2p^2+p+9=m^2
p(2p+1)=(m-3)(m+3)

とまずは変形する。
pは素数なので、m-3またはm+3を割り切る。
なので、場合分けしていく。

①m-3がpの倍数のとき

m-3=pn (n \ge 1)……(1)

とおくと、

2p^2+p=pn(pn+6)
         =n^2p^2+6np

pとp^2でまとめて、

(6n-1)p=(2-n^2)p^2
(6n-1)=(2-n^2)p……(2)

ここで、左辺は正であるから右辺も正でなければいけない。よって、n=1しかありえない。このとき、(1)(2)式より、

p=5
m=8

となる。

②m+3がpの倍数のとき

こちらの方が少し難しい。

m+3=pn (n \ge 1)

とおくと、

2p^2+p=(pn-6)pn
         =n^2p^2-6np

pとp^2でまとめて、

(6n+1)p=(n^2-2)p^2
(6n+1)=(n^2-2)p……(3)

を得る。不等式による絞り込みを使いたいので、素数pによる絞り込みを使う。p=2は題意を満たさないので*1

p\ge 3

である。これを上式に代入して、

(6n+1) \ge 3(n^2-2)

を得る。式変形してf(n)を次のように定義する。

f(n) \equiv 3n^2-6n-7 \le 0……(4)

ここで、

 f(-1)=2 \gt 0
 f(0)=-7 \lt 0
 f(2)=-7 \lt 0
 f(3)= 2 \gt 0

より、上の不等式(4)の解はn\ge1に注意して

1 \le n \le 2

となる。(3)式より、n=1は右辺だけが負になるので不適。n=2は

13=2p

となり、13は偶数ではないので不適。

解答(おわり)

よって、求める解は

p=5,m=8

のみであることがわかった。

 

*1:2 \times 2^2+9 =19は平方数ではない。

【リーマン予想】約数関数を計算してみた

プチ研究 プログラミング 数学

数学関連の絶版本・品切れ本をコチラから購入できます！

約数関数

　自然数Nに対して、約数関数\sigma_x(N)は次のように定義される。

\sigma_x(N)=\sum_{d|N} d^x……①

　つまり、Nの全ての約数のx乗の総和である。詳しくは、約数関数 - Wikipediaを参照。\sigma_1(N)を特に、\sigma(N)と書く。

リーマン予想と約数関数

　wikiによると、この約数関数\sigma(N)が次の不等式を満たすとき、リーマン予想も真であるらしい。

\sigma (N) \lt e^{\gamma} N \log \log N \;  (N \gt 5040) ……②

ここで、\gammaはオイラーの定数(オイラーの定数 - Wikipedia)である。*1
　そこで、具体的に大きなNに対して、上の不等式が成り立つかチェックしてみることにした。

数値計算で求めた約数関数

　Pythonで、約数関数\sigma(N)を計算したものが次の図である。青線が約数関数で、オレンジ色の線が②式の右辺の式である。まずは、N=1000までを見てみた。

f:id:FoxQ:20181229104234p:plain

不等式が成り立たないNがいくつかあるが、まだN \le 5040なので問題ない。
次に、N=5040までを見てみる。

f:id:FoxQ:20181229113059p:plain

N=5040ちょうどでは、不等式は成り立たないことがわかった。

次に、N=10000までを見てみた。

f:id:FoxQ:20181229104442p:plain

②の不等式が成り立っていることが確認できた。さらに、N=100000までを見てみる。

f:id:FoxQ:20181229104550p:plain

　結構きわどいところまで約数関数の値が大きくなっているところもあるが、やはり②の不等式は成り立っている。計算時間の都合上、今回はここまでで計算をやめた。今回計算した範囲では、リーマン予想の反証は得られなかった。

約数関数\sigma_x(N)

 　最後におまけとして、約数関数\sigma_x(N)をxを変えながら、プロットした図も調べてみた。これは、英語版wiki(Divisor function - Wikipedia)に乗っているものの再計算と追加計算になる。以下、N=250までとする。
　まずは、\sigma_0(N)から、

f:id:FoxQ:20181229105243p:plain

これは、約数の個数をカウントしたものになる。ところどころ、値が2になっているところが素数に対応している。\sigma_1(N)から\sigma_5(N)までを一気に見ていこう。

f:id:FoxQ:20181229105530p:plain

f:id:FoxQ:20181229105507p:plain

f:id:FoxQ:20181229105548p:plain

f:id:FoxQ:20181229105603p:plain

f:id:FoxQ:20181229105620p:plain

\sigma_x(N)のxの値が大きくなるにつれ相対的な値のばらつきが小さくなっていくことがわかった。
　x=1のときのN \gt 5040での上限が、②式で与えられることを考えると、N^xになんらかの因子をかけたものが、\sigma_x(N)のNが十分大きいときの上限になると予想される。だが、具体的な式の形は今のところわからない。

*1:ちなみに、オイラーの定数は無理数かどうかすらよくわかっていない謎の多い数である。

合成数へ一般化されたウラムの螺旋

数学 プログラミング プチ研究 オリジナル

数学関連の絶版本・品切れ本をコチラから購入できます！

ウラムの螺旋の一般化

　前回、ウラムの螺旋を描くプログラムを書いたので、それをちょっとだけ改造して何か面白いことができないかと思った。

sky-time-math.hatenablog.jp

　そこで、ウラムの螺旋を一般化してみることにした。つまり、素数の点だけをプロットするのがウラムの螺旋なら、２つの素数の積で表せる数を「2-ウラムの螺旋」と呼べるだろうし、３つの素数の積なら「3-ウラムの螺旋」ができるはずである。
　プログラムの変更は簡単だったので、早速やってみた。

２-ウラムの螺旋

　２つの素数の積で表される合成数のみを螺旋状にプロットしたものが「2-ウラムの螺旋」である。N=100までプロットしてみるとこうなる。２つの素数の積で表される数を黄色、その他の数を緑でプロットしてある。

f:id:FoxQ:20181223115210p:plain

素数が飛び飛びであったのに対して、通常のウラムの螺旋では見られなかった「クラスター」が見られる。N=1000まででは、

f:id:FoxQ:20181223115353p:plain

とやはりクラスターがたくさんできている。N=10000までも見てみる。

f:id:FoxQ:20181223115442p:plain

クラスターがたくさんあって、輪っか状や釣鐘状になっているのがみられる。若干、中央に近い方が大きなクラスターが多いようにも見える。このようにクラスターがたくさんできるというのが「2-ウラムの螺旋」の特徴らしい。

３-ウラムの螺旋

　３つの素数の積で表される数を水色、他の数を緑でプロットしたものをみてみる。
まずは、N=100まで、

f:id:FoxQ:20181223120109p:plain

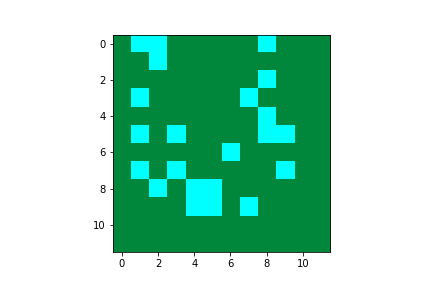
「2-ウラムの螺旋」に対して、クラスターが少し小さくなっている。N=1000までを見てみよう。

f:id:FoxQ:20181223120230p:plain

やはり、クラスターが小さくなっている。最後に、N=10000を見る。

f:id:FoxQ:20181223120458p:plain

「2-ウラムの螺旋」とは対照的に、中央から離れるほど、クラスターのサイズが大きくなっているように見える。また、うっすらと緑の直線が右下から左上へ中央を通っていくようにも見えている。これは、通常のウラムの螺旋のなごりだろうか。

重ねて書いてみた

　通常のウラムの螺旋を赤色、2-ウラムの螺旋を黄色、3-ウラムの螺旋を水色、その他の数を緑にして同時にプロットした図も参考までに載せておく。
　N=100までは

f:id:FoxQ:20181223121005p:plain

中央にある２つの緑が0と1である。N=1000までは、

f:id:FoxQ:20181223121130p:plain

結構カオスな感じになってきたが、最後にN=10000も参考までに載せておく。

f:id:FoxQ:20181223121225p:plain

以上、一般化されたウラムの螺旋のお話でした。「もっとこうしたら面白いかも」とかのアイデアがあったら、言ってほしいです。気が向いたらやってみます。

、

 

【クリスマス】ウラムの螺旋描いてみた

プログラミング 数学

数学関連の絶版本・品切れ本をコチラから購入できます！

ウラムの螺旋

　ウラムの螺旋とは、自然数の螺旋上に並べ素数だけを塗りつぶしたものである。詳しくは、ウラムの螺旋 - Wikipediaを参照。今回描くウラムの螺旋は、数学ガールの秘密ノート整数で遊ぼうを参考にして、0から始まるものにしてある。

数学ガールの秘密ノート/整数で遊ぼう

数学ガールの秘密ノート/整数で遊ぼう

 

 

クリスマスカラーのウラムの螺旋

　今回は、自分でウラムの螺旋を描いてみた。使った言語は、勉強中のPython。せっかくなので、季節に合わせてクリスマスカラーにしてみた。他の配色のウラムの螺旋が欲しい人がいたら、いってくれたら作ります(rgbを指定してくれると作れます)。

　まずは、100までの素数のウラムの螺旋。素数は赤色、合成数は緑で表示してある。

f:id:FoxQ:20181210125828p:plain

次は、1000までのもの。直線上に素数が並んでるように見える。

f:id:FoxQ:20181210125837p:plain

10000までのもの。いくつかの直線に並んだ模様が見える。

f:id:FoxQ:20181210125943p:plain

最後に、100000までのもの。点が細かすぎてよくわからなくなってきたので、ここまでにする。

f:id:FoxQ:20181210130106p:plain

再配布・ご利用について

　完全にフリー素材としますので、好きなものがあったら、ご自由に使用してくださって構いません。

【近似解の見直し】ぺるせんたげさんの数学コンテスト【問Ⅱ】

twitter プチ研究 数学 オリジナル

ぺるせんたげさんの数学コンテストの問Ⅱの解と近似解

　ぺるせんたげさん(@percentage011)が前回取り上げた問題の答えを公開してくれた。

 　そこで、前回作った近似解と比較してみることにした。

sky-time-math.hatenablog.jp

 　まず、P(n)で比較してみる。オレンジが前回作った近似解で、青がぺるせんたげさんの厳密解だ。

f:id:FoxQ:20181104123654p:plain

次に、nP(n)で比較すると、値のずれが目立ってくる。

f:id:FoxQ:20181104123753p:plain

　特に、nが大きくなると、近似解の方が明らかに大きな値を持つようになってきてしまっている。
　このずれがどこからきたのかを考えていたのだが、おそらく前回の記事の(4)式の規格化定数を(6)式で計算したのがまずかったようだ。そこで、今回は規格化定数を本来の正規分布のものに戻すと、どれくらい近似が改良されるのかを見てみることにする。

近似の改良

　前回と同様にして計算するが、サイコロの目の平均値Xが従う分布関数f(X;/mu,\sigma^2)を

f(X;/mu,\sigma^2) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp( - \frac{(X-\mu)^2}{2\sigma^2})……(1)

と近似する。これ以降の計算は、前回の記事と同様である。
　まず、規格化定数の値を見てみると、

\frac{1}{\sqrt{2\pi \sigma^2}} \simeq 0.234……(2)

と前回の1.36より5~6倍ほど小さくなる。*1これを見て、近似は(1)式の正規分布でした方が良いと反省した。改めて、X=1,2,3,4,5,6での値を見積もると、

f(1;\mu,\sigma^2)=f(6;\mu,\sigma^2)\simeq 3.43 \times 10^{-17}……(3)f(1;\mu,\sigma^2)=f(6;\mu,\sigma^2)\simeq 4.66 \times 10^{-7}……(4)f(1;\mu,\sigma^2)=f(6;\mu,\sigma^2)\simeq 0.0543……(5)

 　前回の記事と同様に、これらの値から求める確率P(n)は、

P(n)\simeq \frac{0.543}{5n+1}……(6)

となる。これにパラメータa,\kappa,\gammaを用いた因子をかけて補正することを考える。つまり、

P(n) \simeq \frac{0.543 [1+a \exp (-\kappa(n-1)^\gamma ]}{5n+1}……(7)

として、nの小さい値からパラメータを決定して、最終的な近似式とする。

　P(1)=1より、

a \simeq 10.0……(8)

　P(2)=\frac{1}{2}より、

\kappa \simeq 0.0911……(9)

　P(3) =\frac{1}{3}より、

\gamma \simeq 0.460……(10)

　以上より、

P(n) \simeq \frac{0.543 [1+10 \exp (-0.0911(n-1)^{0.46} ]}{5n+1}……(11)

と近似式が求まった。 

改良版近似式と厳密解の比較

　改めて作った式と厳密解とでP(n)を比較してみる。

f:id:FoxQ:20181104132700p:plain

　前回と同様ほとんど違いが見られない。

　次に、nP(n)を見てみる。オレンジが前回の近似式で、緑が今回の近似式、青が厳密解である。

f:id:FoxQ:20181104134155p:plain

　nが大きいところでの値が若干良くなっているくらいで、思ったほど改善されなかった。さらに大きいn=100くらいまでを見てみる。

f:id:FoxQ:20181104135023p:plain

　厳密解との差がさらに大きくなった。nP(n)のn\rightarrow \inftyでの収束が近似解の場合かなり遅く、厳密解だとかなり早いことがわかった。これは(7)式の形で近似していることからくる限界だろう。
　そして、厳密解の場合の\lim_{n \rightarrow \infty} nP(n)の値はどうやら0.1よりも小さいようなので、前回の近似で得られる

\lim_{n \rightarrow \infty} nP(n) =0.632……(12)

は明らかに不適だとわかる。今回の近似では、十分大きなnをとる必要があり、収束も遅いものの、

\lim_{n \rightarrow \infty} nP(n) = 0.1086……(13)

なので、まだマシだと言えるだろう。厳密解の値を見ていても、私には本当の\lim_{n \rightarrow \infty} nP(n)の値がわからないので真実は謎のままだ。

*1:この記事では、有効数字3桁で計算していく。