合成数へ一般化されたウラムの螺旋
ウラムの螺旋の一般化
前回、ウラムの螺旋を描くプログラムを書いたので、それをちょっとだけ改造して何か面白いことができないかと思った。
そこで、ウラムの螺旋を一般化してみることにした。つまり、素数の点だけをプロットするのがウラムの螺旋なら、2つの素数の積で表せる数を「2-ウラムの螺旋」と呼べるだろうし、3つの素数の積なら「3-ウラムの螺旋」ができるはずである。
プログラムの変更は簡単だったので、早速やってみた。
2-ウラムの螺旋
2つの素数の積で表される合成数のみを螺旋状にプロットしたものが「2-ウラムの螺旋」である。までプロットしてみるとこうなる。2つの素数の積で表される数を黄色、その他の数を緑でプロットしてある。

素数が飛び飛びであったのに対して、通常のウラムの螺旋では見られなかった「クラスター」が見られる。まででは、

とやはりクラスターがたくさんできている。までも見てみる。

クラスターがたくさんあって、輪っか状や釣鐘状になっているのがみられる。若干、中央に近い方が大きなクラスターが多いようにも見える。このようにクラスターがたくさんできるというのが「2-ウラムの螺旋」の特徴らしい。
3-ウラムの螺旋
3つの素数の積で表される数を水色、他の数を緑でプロットしたものをみてみる。
まずは、まで、
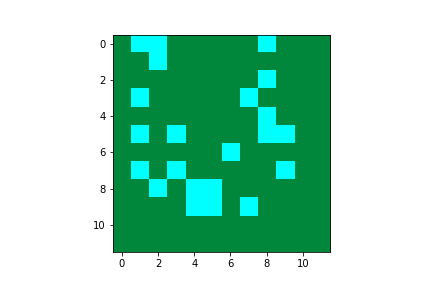
「2-ウラムの螺旋」に対して、クラスターが少し小さくなっている。までを見てみよう。

やはり、クラスターが小さくなっている。最後に、を見る。

「2-ウラムの螺旋」とは対照的に、中央から離れるほど、クラスターのサイズが大きくなっているように見える。また、うっすらと緑の直線が右下から左上へ中央を通っていくようにも見えている。これは、通常のウラムの螺旋のなごりだろうか。
重ねて書いてみた
通常のウラムの螺旋を赤色、2-ウラムの螺旋を黄色、3-ウラムの螺旋を水色、その他の数を緑にして同時にプロットした図も参考までに載せておく。
までは

中央にある2つの緑が0と1である。までは、

結構カオスな感じになってきたが、最後にも参考までに載せておく。

以上、一般化されたウラムの螺旋のお話でした。「もっとこうしたら面白いかも」とかのアイデアがあったら、言ってほしいです。気が向いたらやってみます。
、