【素数判定】自然数の分解に基づく素数判定遊び【Python】
事始め
覚えてないですよね^_^一昨年あたりに数学デーでひたすら僕のアマチュア数学研究テーマを書き連ねて説明してた奴です^_^
— ひさぴょん@勉強垢 (@o_hisashi) 2021年9月18日
式としてはこんなのです。
53=2^2×3×5-7
67=2×5×7-3
一目で素数ってわかるよね?ってやつ。
上記のひさぴょんさんの素数判定法が面白かったので、インスピレーションが湧いた。
397の素数判定式
397は一つの都合のいい素数の和差積であらわすことができないことが考えられているそうだ。ツイート内の引RT内の文献参照のこと。
そこで、2つの素数の和差積で表すことにして、実際成功した。
√397<20に注意して、
— FoxQ@楕円曲線を囲む会@表現者@物理学者@フォロバ99% (@foxq0113) 2021年9月18日
397=2^3×11×19-3×5^2×17⇒2,3,5,11,17,19の倍数でない。
397=2^2×7×13+3×11⇒2,3,7,11,13の倍数でない。
よって、397は素数。
式2つまで減らせた。 https://t.co/K3iwZoSPBm
インスピレーションを受けて
今回の手法のポイントは2つの和か差の数に分けて、各数が多くの素数の積になっていて、なおかつそれら2数が互いに素であるということである。つまり、ツイートにまとめたように、
Nがk種類の素因数を持つ期待値をP(N)と書いた時、
— FoxQ@楕円曲線を囲む会@表現者@物理学者@フォロバ99% (@foxq0113) 2021年9月18日
N=M±Lで、gcd(M,L)=1とする。
このとき、Nが素数になる確率p(N)は、
p(N)=(P(M)+P(L))/(√N以下の素数の個数)
=(P(M)+P(L)))/π(√N)
と見積もれる。後は、P(N)はπ(√N)-P(M)-P(L)で近似できるかな……
のように見積もれることになる。
実装
乱数で素数判定の式を2つに分けて、素因数の種類はなるべく大きくなるように更新すると、以下のようなプログラムになる。
2~10までの素数判定および素因数の種類数を既知として、10~1000までの素数判定を行った結果が次のものである。
gistf734d8d9838e28e061a878ce13489e0c
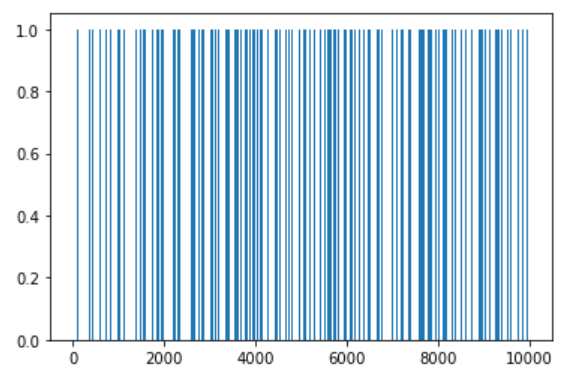
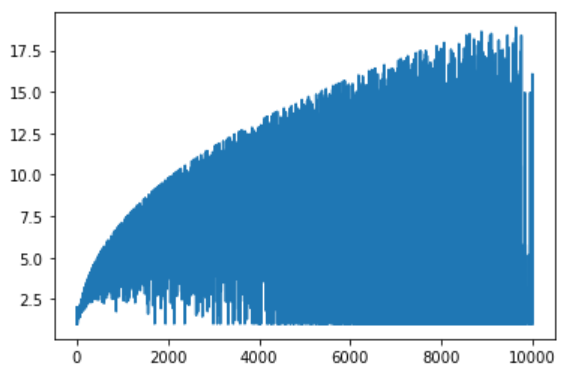
合成数と素数の判定成功率は約47%で、素数だけで判定成功確率を見ると約55%となっている。また、素因数の種類の推測値も同時にプロットされている。図では、値が1のところが正しく判定できている。
今回のケースは、1~1000までに素数は、168個あり、その内90個の判定に成功している。
1~1万までの数を対象に素数判定しても、合成数と素数の判定成功率は約49%で、素数だけで判定成功確率を見ると約56%となり、数の大きさの増加に対してある程度安定性があることがわかった。
このケースは、1~1万までに素数は、1229個あり、その内680個の判定に成功している。
まとめ
今回の推論モデルは、素因数の種類を確率的に見積もることで、そこから素数判定を行うものだった。成功確率は安定して55%付近となっており、素数の個数が減ってきても判定にはさほど影響を及ぼさないことが分かった。