2020-08-14

【Kindle】素数表100万個プログラムつき【Python】

｢素数表100万個プログラムつき｣、ワンコインで出版しました!!

f:id:FoxQ:20200814120023j:plain

https://amazon.co.jp/dp/B08FTBSL25

素数1万個あたり5円です!! 数時間プログラムを動かせば、1万個あたり0.5円となり更にお得ですよ!! Windowsでもjupyter notebookインストールしたら、Pythonで動きます。

最初の11万334個の素数は試し読みが出来るので、ぜひダウンロードしてみてください。検索機能で、素数判定などできます。

2020-08-11

【初めての数学書】多点総和法入門が出版されました!!【Kindle】

2点総和法オリジナルプチ研究数学 Kindle

僕の初めての数学書が出版されました!!

多点総和法入門高校生でもわかる！！ココと無限のかなたをつなぐ現代応用数学: テイラー展開から微分方程式の応用まで | 上岡良季 | 数学 | Kindleストア | Amazon

f:id:FoxQ:20200811020526j:plain

内容は、まず中・高数学の復習から始まり、大学数学への入門(テイラー展開、パデ近似)を丁寧に新しい視点で説明します。そしてそれらを更に発展させた現代的な応用数学である、2点パデ近似から多点総和法へと話は進みます!!
2点パデ近似を用いた、各種特殊関数の近似や、微分方程式の近似解法やリーマンζ関数の非自明な零点の近似的見積もりへの応用もあります!!

ぜひ、ご一読を!!

2020-07-21

【その２】特異点のある関数の2点漸近展開に対する総和法【多項式型】

オリジナルプチ研究数学 2点総和法

Amazon.co.jp: Yoshiki Ueoka:作品一覧、著者略歴

数学関連の絶版本・品切れ本をコチラから購入できます！

特異点

この記事は前回の2点パデ近似の続きである。今回の記事では特異点の取り扱い方について説明する。

sky-time-math.hatenablog.jp

特異点は、もしあれば、関数の振る舞いを大きく特徴づける重要な情報である。そこで、今回は関数 $f(x)$ が自然数のべきの孤立特異点 *1を持つ場合、すなわち、 $x=x_1,x_2,\cdots,x_m$

$f(x)\rightarrow \frac{A_j}{(x-x_j)^{n_j}} (x\rightarrow x_j)$

となる場合を考える。このとき、

$g_*(x):=f(x)-\sum_{j=1}^m \frac{A_j}{(x-x_j)^{n_j}}$

は、 $x=\infty$ を除いて特異点を持たないので、

$g_*(x)$ の漸近展開を

$g_*(x)\sim g_0(x) +O(g_0(x))(x\rightarrow 0)$

$g_*(x)\sim g_\infty(x) +o(g_\infty(x))(x\rightarrow \infty)$

と計算する。ここで、パデ近似を適用するために多項式型の因子を引き出して、

$g_*(x)=:\frac{1}{\prod_{j=1}^m(x-x_j)^{n_j}}g(x)$

とすると、 $g(x)$ は $x=\pm \infty$ 以外で、特異点を持たない。

$g(x)$ に対する2点パデ近似を $G(x)$ とすると、 $f(x)$ の特異点を考慮した2点パデ近似 $F_*(x)$ は、

$F_*(x)=\sum_{j=1}^m \frac{A_j}{(x-x_j)^{n_j}}+\frac{G(x)}{\prod_{j=1}^m(x-x_j)^{n_j}}$

となる。ここで、 $c_j$ は、各特異点での発散のスピード $A_j$ を再現するように決定する。

詳しくは、拙著、多点総和法入門を読んでいただきたい。

多点総和法入門高校生でもわかる！！ココと無限のかなたをつなぐ現代応用数学: テイラー展開から微分方程式の応用まで

作者:上岡　良季
発売日: 2020/07/28
メディア: Kindle版

実際の例

それでは、前回の記事で2点パデ近似を適用した関数 $f(x)$ に対して、

$f(x)=\frac{2+3x+4x^2+5x^3+6x^4}{1+x+x^2+x^3}$

その特異点、

$f(x) \sim \frac{2}{x+1} (x\rightarrow -1)$

を取り入れた2点パデ近似*2を実際にやってみよう。まず、関数 $g_*(x)$ の2点での漸近展開は

$g_*(x)\sim −\frac{2}{x+1}+2+x+x^2+O(x^3) (x\rightarrow 0)$

$=\frac{2}{x+1}(\frac{3}{2}x+x^2+\frac{1}{2}x^3+O(x^4)) (x\rightarrow 0)$

$g_*(x)\sim \frac{2}{x+1}(3x^2+\frac{5}{2}x-\frac{3}{2}+o(1)) (x\rightarrow 0)$

ここで、特異点の因子 $\frac{2}{x+1}$ を除いて $x\rightarrow \infty$ での項を分離すると、

$G(x)\approx (3x^2+\frac{5}{2}x-\frac{3}{2})+(\frac{3}{2}-x-2x^2+\frac{1}{2}x^3)$

となるので、2点パデ近似はパデ近似 $[1/2]$ を第二項に適用して、

$G(x)\approx (3x^2+\frac{5}{2}x-\frac{3}{2})+\frac{48-47x}{36x^2-10x+32}$

となる。これは、次の漸近展開を持つ。

$G(x)=\frac{3}{2}x+x^2 +\frac{1}{2}x^3+O(x^4) (x\rightarrow 0)$

$G_(x)\sim 3x^2+\frac{5}{2}x-\frac{3}{2}x+o(1) (x\rightarrow 0)$

これを用いて、特異点を取り入れた2点パデ近似 $F_*(x)$ は、

$F_*(x)=\frac{2}{x+1}+\frac{2}{x+1}G(x)$

$=\frac{2}{x+1}(3x^2+\frac{5}{2}x-\frac{1}{2} +\frac{48-47x}{36x^2-10x+32} )$

となる。この関数は次の漸近展開を持つ。

$F_*(x)\sim 2+x+x^2+O(x^3) (x\rightarrow 0)$

$F_*(x)\sim 6x-1 +o(1) (x\rightarrow \infty)$

ここで、注意しなければいけないのは、

$lim_{x\rightarrow -1} F_*(x)\frac{x+1}{2}=\frac{95}{78}$

となり特異点の振る舞いを完全には取り入れきれないことである。ただ、 $x=-1$ で係数 $2$ に近い値で発散することのみ記述されている。

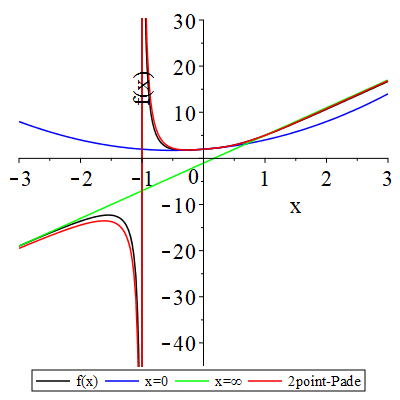
それでは、特異点を取り入れた2点パデ近似をプロットしたものを見てみよう。

f:id:FoxQ:20200721172048p:plain

今回は、 $x=-1$ 以外の特異点がたまたま存在せず、特異点を取り入れた2点パデ近似が非常によい近似となっていることがわかる。

*1:有理数の場合も変数変換を用いれば同様の解析が可能である。

*2:特異点も入れているので、3点パデ近似と呼んでもいいかもしれない。

2020-07-21

【その１】2点漸近展開に対する総和法【多項式型】

オリジナルプチ研究数学 2点総和法

Amazon.co.jp: Yoshiki Ueoka:作品一覧、著者略歴

数学関連の絶版本・品切れ本をコチラから購入できます！

2点での漸近展開

この記事に続く一連の記事で、ある実関数 $f(x)$ の $x=0$ と $x=\infty$ での漸近展開がそれぞれ得られた時の総和法を紹介する。すなわち、

$f(x)\sim f_0(x)+o(f_0(x)) (x\rightarrow 0)$

$f(x)\sim f_\infty(x)+o(f_\infty(x)) (x\rightarrow 0)$

という漸近展開が与えられた時、与えられた情報の範囲でこれを再現するような簡単な関数 $F(x)$ を見つけることを目的とする。この手法は、僕が博士論文を書く時に開発した手法をより簡単にしたものや一般化したものにあたる。基本的な発想は今回の記事を読んでもらえればわかると思うが、今後このシリーズを通して、様々な応用が可能な有用な手法であることをお見せしたい。

詳しくは、拙著、多点総和法入門を読んでいただきたい。

多点総和法入門高校生でもわかる！！ココと無限のかなたをつなぐ現代応用数学: テイラー展開から微分方程式の応用まで

作者:上岡　良季
発売日: 2020/07/28
メディア: Kindle版

2点パデ近似

今回紹介する最も簡単な方法を、「2点パデ近似」と名づけることにする。今回はさらに $x\rightarrow \infty$ での漸近展開が多項式で与えられる場合を考える。

つまり、関数 $f(x)$ の漸近展開が、

$f(x)\sim a_0+a_1x+a_2x^2+\cdots+a_nx^n+O(x^{n+1}) (x \rightarrow 0)$

$f(x)\sim b_mx^m+b_{m-1}x^{m-1}+\cdots b_lx^l+o(x^l) (x \rightarrow \infty)$

で与えられる場合を考える。そして、この2点での漸近展開を同時に再現する簡単な関数を総和法の一種であるパデ近似を駆使して見つける。以下、それぞれの多項式部分を $f_0(x),f_\infty(x)$ とおくと約束する。

漸近項の分離

近似する関数をまずは、

$F(x)\approx f_\infty(x)+(f_0(x)-f_\infty(x))$

と表し、第二項を分子が $N$ 次多項式で、分母が $M$ 字多項式のパデ近似 $[N/M](x)$ で近似する。すると、

$F(x)\approx f_\infty(x)+[N/M](x)$

ここで、

$N-M \lt l$

となるようにパデ近似の次数を選ぶと、 $x\rightarrow \infty$ での漸近展開は明らかに

$F(x)\sim f_\infty(x)+o(x^l) (x\rightarrow \infty)$

となる。また、パデ近似は、 $x\rightarrow 0$ での展開を与えられた次数まで再現する近似なので、 $x\rightarrow 0$ での漸近展開は、当然

$F(x)\sim f_0(x)+O(x^{n+1}) (x\rightarrow \infty)$

となる。

例

練習として、

$f(x)=\frac{2+3x+4x^2+5x^3+6x^4}{1+x+x^2+x^3}$

の場合をやってみせよう。この関数を特徴づけるパラメータは8個である。つまり、この関数を近似するより簡単な式を見つけたい。

この関数の2点での漸近展開を2次までとるとすると、

$f(x) \sim 2+x+x^2 +O(x^3) (x\rightarrow 0)$

$f(x) \sim 6x-1 +o(1) (x\rightarrow \infty)$

となる。まず、それぞれのグラフを見てみよう。

f:id:FoxQ:20200721205847p:plain — f(x)とその漸近展開

黒線が関数 $f(x)$ で、青と緑がそれぞれ、 $x=0,\infty$ における漸近展開を有限次で打ち切った近似である。各漸近展開が、それぞれの展開点から離れるに従って、破綻するのがみてとれるだろう。

まず $F(x)$ を

$F(x)=(6x-1)+\{(2+x+x^2)-(6x-1)\}$

$=(6x-1)+(3-5x+x^2)$

ここで、 $o(1)$ となるような第二項のパデ近似は $[0/2](x)$ である。実際に、Wolfram AlphaやMapleなどを使って計算すると、

$F(x)\approx 6x-1 +\frac{27}{22x^2+15x+9}$

となる。このようにして、関数 $f(x)$ の2点までの漸近展開を2次まで再現する関数を得ることができた。実際にプロットした図を見てみよう。赤色の線が2点パデ近似 $F(x)$ である。

f:id:FoxQ:20200721144928p:plain — 2点パデ近似(x=0~3)

このように、 $x=0,\infty$ の両方で大きく破綻することないよい近似を与えていることがわかる。

特異点

さて、今回得た近似 $F(x)$ はパデ近似を用いているが特異点をたまたま持たない*1。ところが元の関数 $f(x)$ は特異点を持つ。実際にどうなっているか見てみよう。

f:id:FoxQ:20200721145716p:plain — 2点パデ近似と特異点

このように単純な総和法を用いると、特異点を再現することに失敗する。次回の記事では、特異点を再現する2点パデ近似を紹介する。

sky-time-math.hatenablog.jp

*1:一般には2点パデ近似は特異点を持つ。そのため、連続関数を近似したい場合、更にボレル総和法と組み合わせた2点ボレル-パデ近似(僕が名づけた)を用いる必要がある。

2019-11-02

【後編】FoxQの観賞用問題1【第１２回関西すうがく徒のつどい】

数学オリジナル第１２回関西すうがく徒のつどい

数学関連の絶版本・品切れ本をコチラから購入できます！

【後編】FoxQの予想の部分的証明(素数で表される場合 )

$k,n$ を自然数としたとき、

$p^a+(2^k q)^b=n^2$ ……①

を満たす素数 $p,q$ と自然数 $k,a,b$ の組を求めよ。ただし、 $(p,2^k q)$ は原始ピタゴラス数の内小さい方の2組とする。twitterの問題も貼っておきます。

[FoxQの鑑賞用問題1(解答は第12回つどい参加者限定です。)]
p,qを素数、n,k,a,bを自然数とし、次の式を考える。

p^a+[(2^k)q]^b=n^2……①

p,(2^k)qが原始ピタゴラス数の内の小さい2数のとき、①式を満たす(p,q,k,a,b)の組を全て求めよ。#kansaimath
— FoxQ (@foxq_stm) October 26, 2019

原始ピタゴラス数の小さい方の2組の内、一方は $3$ の倍数なので、

$p=3$ または $q=3$

である。今回の記事【後編】では $p=3$ の場合を取り扱う。
原始ピタゴラス数の小さい2数の内、一方は4の倍数なので、 $q=2$ または $k\ge 2$ が成り立つ。そこで、法を $4$ として、①式を書き出すと、

$3^a\equiv n^2 (\bmod 4)$ ……(1.0)

より、 $a$ は偶数である。 $p,2^kq$ は原始ピタゴラス数の小さい2数であったので、自然数 $s,t (s \gt t)$ を用いて、

$3=s^2-t^2=(s-t)(s+t)$ ……(1.1)
$2st=2^kq\Rightarrow st=2^{k-1}q$ ……(1.2)

となるので、可能な $s,t$ の組み合わせは、

(i) $s=2^{k-1}q,t=1$
(ii) $s=2^{k-1},t=q$
(iii) $s=q,t=2^{k-1}$

まず、(i)は(1.1)式より、

$3=2^{2k-2}q^2-1$ ……(1.3)

となるが、これを満たすのは、 $k=1,q=2$ のみである。

次に、(ii)も(1.1)式より、因数分解の形になっているので、

$2^{k-1}-q=1,2^{k-1}+q=3$
$\Rightarrow q=2^{k-1}-1,2^{k-1}+q=3$
$\Rightarrow 2^k=4$
$\Rightarrow k=2$
$\Rightarrow q=2^{2-1}-1=1$ ……(1.4)

となり矛盾。

最後に、(iii)も(1.1)式より、因数分解の形になっているので、

$q-2^{k-1}=1,q+2^{k-1}=3$
$\Rightarrow q=2^{k-1}+1,2^{k-1}+q=3$
$\Rightarrow 2^k=2$
$\Rightarrow k=1$
$\Rightarrow q=2^{1-1}+1=2$ ……(1.5)

以上より、(i)(ii)(iii)から、

$k=1,q=2$ ……(1.6)

が言えた。従って、解くべき方程式は、

$3^a+4^b=n^2$ ……(1.7)

$3^a+4^b=n^2$ を解く。

まずは、式変形する。

$3^a+(2^b)^2=n^2$
$\Rightarrow 3^a=(n-2^b)(n+2^b)$ ……(2.1)

ここで、 $(n+2^b)-(n-2^b)=2^{b+1}$ より、 $n+2^b$ と $n-2^b$ との公約数は $2^{b+1}$ の約数であるが、これは $3$ と互いに素なので、

$n-2^b=1,n+2^b=3^a$
$\Rightarrow 2^{b+1}=3^a-1$ ……(2.2)

一方、(1.0)式より、 $a$ は偶数であったので、 $a=2c$ とおいて最初の式を変形すると、

$4^b=(n-3^c)(n+3^c)$ ……(2.3)

ここで、 $(n+3^c)-(n-3^c)=2\cdot3^{c}$ より、 $n+3^b$ と $n-3^b$ との公約数は $2\cdot3^c$ の約数であり、 $n$ が奇数であることから $n+3^b$ と $n-3^b$ は偶数となり、

$n-3^c=2,n+3^c=2^{2b-1}$
$\Rightarrow 2\cdot 3^c=2^{2b-1}-2$
$\Rightarrow 3^c=2^{2b-2}-1$ ……(2.4)

ここで、両辺を2乗して、 $a=2c$ であったことを思い出すと、

$3^a=2^{4b-4}-2\cdot 2^{2b-2}+1$ ……(2.5)

この式を(2.2)式と比較して、

$2^{b+1}+1=2^{4b-4}-2\cdot 2^{2b-2}+1$
$\Rightarrow 2^{b+1}=2^{4b-4}-2\cdot 2^{2b-2}$
$\Rightarrow 0=2^{4b}-2^3\cdot 2^{2b}-2^5\cdot 2^b$
$\Rightarrow 0=2^{3b}-8\cdot 2^{b}-32$ ……(2.6)

ここで、 $x=2^b$ とおくと、

$0=x^3-8x-32$ ……(2.7)

を得る。 $x=4$ はこの方程式の解なので、因数分解して、

$0=(x-4)(x^2+4x+8)$ ……(2.8)

ここで、 $x^2+4x+8=0$ の判別式 $D$ は、

$D/4=2^2-8=-4\lt 0$ ……(2.9)

なので、(2.8)式は $x=4$ 以外の解を持たない。即ち、

$x=4=2^b\Rightarrow b=2$ ……(2.10)

ここで、(2.4)式より、

$3^c=2^{2\cdot 2-2}-1=2^2-1=3 \Rightarrow c=1$
$\Rightarrow a=2c=1$ ……(2.11)

よって、求める解は、

$(p,q,k,a,b)=(3,2,1,2,2)$

前編はこちらへ。

sky-time-math.hatenablog.jp

2019-11-02

【前編】FoxQの観賞用問題1【第１２回関西すうがく徒のつどい】

数学オリジナル第１２回関西すうがく徒のつどい

数学関連の絶版本・品切れ本をコチラから購入できます！

FoxQの予想の部分的証明(素数で表される場合 )

$n$ を自然数としたとき、

$p^a+(2^k q)^b=n^2$ ……①

を満たす素数 $p,q$ と自然数 $k,a,b$ の組を求めよ。twitterの問題も貼っておきます。ただし、 $(p,2^k q)$ は原始ピタゴラス数の内小さい方の2組とする。

[FoxQの鑑賞用問題1(解答は第12回つどい参加者限定です。)]
p,qを素数、n,k,a,bを自然数とし、次の式を考える。

p^a+[(2^k)q]^b=n^2……①

p,(2^k)qが原始ピタゴラス数の内の小さい2数のとき、①式を満たす(p,q,k,a,b)の組を全て求めよ。#kansaimath
— FoxQ (@foxq_stm) October 26, 2019

原始ピタゴラス数の小さい方の2組の内、一方は $3$ の倍数なので、

$p=3$ または $q=3$

である。今回の記事【前編】では $q=3$ の場合を取り扱う。
$q=3$ のとき、 $(p,2^k q)$ は原始ピタゴラス数であったので、互いに素な奇数 $s,t(s \gt t)$ を用いて、

$p=st\Rightarrow s=p,t=1$ ……(1.1)
$2^k \cdot 3=\frac{(s-t)(s+t)}{2}=\frac{p^2-1^2}{2}$ ……(1.2)

これより、

$2^{k+1}\cdot 3=p^2-1=(p-1)(p+1)$ ……(1.3)

ここで、 $(p+1)-(p-1)=2$ で、 $p$ は明らかに $2$ でないので、奇素数である。よって、 $p-1$ が偶数で、 $p-1$ と $p+1$ の公約数が2以下であることから、

(i) $p-1=2,p+1=2^k\cdot 3$
(ii) $p-1=2^k,p+1=2\cdot 3$
(iii) $p-1=2\cdot 3, p+1=2^k$

と場合分けできる。

(i)の場合、2つの式の差をとって、

$2=2^k\cdot 3 -2\Rightarrow 1=2^{k-1}\cdot 3 -1$ ……(1.4)

となるがこれをみたす $k$ は存在しないので矛盾。

(ii)の場合、2つの式の差をとって、

$2=2\cdot 3 -2^k \Rightarrow 1=3-2^{k-1}$ ……(1.5)

これを満たす $k$ は、 $k=2$ 。
このとき、(ii)式より $p=5$ 。従って、①式は、

$5^a+12^b=n^2$ ……(1.6)

となる。

(iii)の場合、2つの式の差をとって、

$2=2^k-2\cdot 3\Rightarrow 1=2^{k-1}-3$ ……(1.7)

これを満たす $k$ は、 $k=3$ 。
このとき、(iii)式より $p=7$ 。従って、①式は、

$7^a+24^b=n^2$ ……(1.8)

となる。

$5^a+12^b=n^2$ を解く。

法を $5$ とすると、

$2^b\equiv n^2 (\bmod 5)$ ……(2.1)

となるので、 $b$ は $4$ の倍数でなければならない。特に、 $b$ は偶数である。
次に、法を $3$ とすると、

$5^a\equiv n^2 (\bmod 3)$ ……(2.2)

となるので、 $a$ も偶数である。

よって、自然数 $c,d$ を用いて、 $a=2c,b=2d$ と置き直すと、

$(5^c)^2+(12^d)^2=n^2$ ……(2.3)

ここで、 $5$ と $12$ は互いに素なので、 $5^c,12^d,n$ は原始ピタゴラス数となっている。従って、互いに素な自然数 $s,t(s \gt t )$ が存在して、

$5^c=s^2-t^2$ ……(2.4)
$12^d=2st\Rightarrow st=2^{2d-1}3^d$ ……(2.5)

となる。 $s,t$ の可能な場合分けは、

(i) $s=2^{2d-1}3^d,t=1$
(ii) $s=2^{2d-1},t=3^d$
(iii) $s=3^d,t=2^{2d-1}$

である。(2.4)式より、法を $4$ とすると(i)は

$1\equiv 5^c \equiv 2^{4d-2}3^{2d}-1\equiv -1 (\bmod 4)$ ……(2.6)

となり、矛盾。同様に、(2.4)式より、法を $4$ とすると、(ii)は

$1\equiv 5^c \equiv 2^{4d-2}-3^{2d}\equiv -1^{2d} \equiv -1 (\bmod 4)$ ……(2.7)

となり矛盾。(iii)は、 $s \gt t$ の条件より、

$d=1,2$ ……(2.8)

まず、 $d=1$ のとき、[s=3,t=2]より、(2.4)式から

$5^c=3^2-2^2=5$ ……(2.9)

より、 $c=1$ 。

次に $d=2$ のとき、

$5^c=9^2-8^2=17$ ……(2.10)

となるので矛盾。以上より、

$5^a+12^b=n^2$ ……(2.11)

の解は $a=2c=2,b=2d=2$ のみであることがわかった。

$7^a+24^b=n^2$ を解く。

まず、法を $4$ にとって、

$7^a\equiv(-1)^a\equiv n^2$ ……(3.1)

より、 $a$ は偶数でなければいけない。
次に、法を $7$ にとると、

$n^2\equiv 1,4,2,0 (\bmod 7)$ ……(3.2)

また、 $b=1,2,3,4,5,6,\cdots$ に対して、それぞれ

$24^b\equiv 3^b\equiv 3,2,6,4,5,1,\cdots(\bmod 7)$ ……(3.3)

となるので、 $b$ も偶数である。よって、自然数 $c,d$ を用いて、 $a=2c,b=2d$ と置き直すと、

$(7^c)^2+(24^d)^2=n^2$ ……(3.4)

ここで、 $7$ と $24$ は互いに素なので、 $7^c,24^d,n$ は原始ピタゴラス数となっている。従って、互いに素な自然数 $s,t(s \gt t )$ が存在して、

$7^c=s^2-t^2=(s-t)(s+t)$ ……(3.5)
$24^d=2st\Rightarrow st=2^{3d-1}3^d$ ……(3.6)

これより、可能な $s,t$ の組み合わせは、

(i) $s=2^{3d-1}3^d,t=1$
(ii) $s=2^{3d-1},t=3^d$

である。(i)は(3.5)式より、法 $3$ とすると、

$1\equiv 7^c\equiv 2^{3d-1}3^d-1\equiv -1 (\bmod 3)$ ……(3.7)

となり矛盾。(ii)は、(3.5)式より、

$7^c=(2^{3d-1}-3^d)(2^{3d-1}+3^d)$ ……(3.8)

ここで、 $(2^{3d-1}+3^d)-(2^{3d-1}-3^d)=2\cdot 3^d$ より、 $2^{3d-1}+3^d$ と $2^{3d-1}-3^d$ の公約数が $2\cdot 3^d$ となるが、これは $7$ と互いに素なので、

$2^{3d-1}-3^d=1$ ……(3.9)
$2^{3d-1}+3^d=7^c$ ……(3.10)

ここで、 $d\ge 2$ と仮定すると、(3.9)式より、法を $2^5=32$ として、 $d=1,2,3,\cdots$ に対して、

$3^d\equiv 3,9,27,17,19,25,11,1,\cdots$ ……(3.11)

となるので、(3.9)式は法を $2^5=32$ として成り立たない。従って、 $d\ge 2$ は矛盾。 $d=1$ のとき、(3.10)式より、

$4+3=7=7^c\Rightarrow c=1$ ……(3.12)

以上より、 $7^a+24^b=n^2$ の解は、

$a=2c=2,b=2d=2$ ……(3.13)

のみであることがわかった。

$q=3$ の場合の求める解

$q=3$ の場合の求める解は、

$(p,q,k,a,b)=(5,3,2,2,2),(7,3,3,2,2)$

後編はこちらから。

sky-time-math.hatenablog.jp

2019-10-27

【第１２回関西すうがく徒のつどい】FoxQからの挑戦状１【解答】

オリジナル数学第１２回関西すうがく徒のつどい

数学関連の絶版本・品切れ本をコチラから購入できます！

FoxQからの挑戦状１

挑戦状シリーズ第一弾です。今回は複数題にわけることで難易度調整してみました。みなさん、問題を楽しんでいただけたでしょうか？楽しんでいただけたなら、とっても嬉しいです。では、問題のおさらいです。

$p,q,r$ を素数、 $k$ を自然数とし次の式を考える。

$p^2+(2^k q)^2=r^2$ ……①

(1) $k=1$ のとき、①式を満たす $p,q,r$ を全て求めよ。
(2) $k=2$ のとき、①式を満たす $p,q,r$ を全て求めよ。
(3) $k\ge 3$ のとき、①式を満たす $p,q,r$ は存在しないことを示せ。

twitterの問題も張り付けておきます。

[FoxQからの挑戦状1(解答は第12回つどい参加者限定です)]
p,q,rを素数、kを自然数とし、次の式を考える。

p^2+[(2^k)q]^2=r^2……①

(1)k=1のとき、①式を満たすp,q,rを求めよ。
(2)k=2のとき、①式を満たすp,q,rを求めよ。
(3)k≧3のとき、①式を満たすp,q,rは存在しないことを示せ。#kansaimath
— FoxQ (@foxq_stm) October 26, 2019