流れる空の中で数学を。

とある数学好きの「手作りすうがく」と「気ままな雑記」。

【その２】特異点のある関数の2点漸近展開に対する総和法【多項式型】

オリジナルプチ研究数学 2点総和法

Amazon.co.jp: Yoshiki Ueoka:作品一覧、著者略歴

数学関連の絶版本・品切れ本をコチラから購入できます！

特異点

この記事は前回の2点パデ近似の続きである。今回の記事では特異点の取り扱い方について説明する。

sky-time-math.hatenablog.jp

特異点は、もしあれば、関数の振る舞いを大きく特徴づける重要な情報である。そこで、今回は関数 $f(x)$ が自然数のべきの孤立特異点 *1を持つ場合、すなわち、 $x=x_1,x_2,\cdots,x_m$

$f(x)\rightarrow \frac{A_j}{(x-x_j)^{n_j}} (x\rightarrow x_j)$

となる場合を考える。このとき、

$g_*(x):=f(x)-\sum_{j=1}^m \frac{A_j}{(x-x_j)^{n_j}}$

は、 $x=\infty$ を除いて特異点を持たないので、

$g_*(x)$ の漸近展開を

$g_*(x)\sim g_0(x) +O(g_0(x))(x\rightarrow 0)$

$g_*(x)\sim g_\infty(x) +o(g_\infty(x))(x\rightarrow \infty)$

と計算する。ここで、パデ近似を適用するために多項式型の因子を引き出して、

$g_*(x)=:\frac{1}{\prod_{j=1}^m(x-x_j)^{n_j}}g(x)$

とすると、 $g(x)$ は $x=\pm \infty$ 以外で、特異点を持たない。

$g(x)$ に対する2点パデ近似を $G(x)$ とすると、 $f(x)$ の特異点を考慮した2点パデ近似 $F_*(x)$ は、

$F_*(x)=\sum_{j=1}^m \frac{A_j}{(x-x_j)^{n_j}}+\frac{G(x)}{\prod_{j=1}^m(x-x_j)^{n_j}}$

となる。ここで、 $c_j$ は、各特異点での発散のスピード $A_j$ を再現するように決定する。

詳しくは、拙著、多点総和法入門を読んでいただきたい。

多点総和法入門高校生でもわかる！！ココと無限のかなたをつなぐ現代応用数学: テイラー展開から微分方程式の応用まで

多点総和法入門高校生でもわかる！！ココと無限のかなたをつなぐ現代応用数学: テイラー展開から微分方程式の応用まで

作者:上岡　良季
発売日: 2020/07/28
メディア: Kindle版

実際の例

それでは、前回の記事で2点パデ近似を適用した関数 $f(x)$ に対して、

$f(x)=\frac{2+3x+4x^2+5x^3+6x^4}{1+x+x^2+x^3}$

その特異点、

$f(x) \sim \frac{2}{x+1} (x\rightarrow -1)$

を取り入れた2点パデ近似*2を実際にやってみよう。まず、関数 $g_*(x)$ の2点での漸近展開は

$g_*(x)\sim −\frac{2}{x+1}+2+x+x^2+O(x^3) (x\rightarrow 0)$

$=\frac{2}{x+1}(\frac{3}{2}x+x^2+\frac{1}{2}x^3+O(x^4)) (x\rightarrow 0)$

$g_*(x)\sim \frac{2}{x+1}(3x^2+\frac{5}{2}x-\frac{3}{2}+o(1)) (x\rightarrow 0)$

ここで、特異点の因子 $\frac{2}{x+1}$ を除いて $x\rightarrow \infty$ での項を分離すると、

$G(x)\approx (3x^2+\frac{5}{2}x-\frac{3}{2})+(\frac{3}{2}-x-2x^2+\frac{1}{2}x^3)$

となるので、2点パデ近似はパデ近似 $[1/2]$ を第二項に適用して、

$G(x)\approx (3x^2+\frac{5}{2}x-\frac{3}{2})+\frac{48-47x}{36x^2-10x+32}$

となる。これは、次の漸近展開を持つ。

$G(x)=\frac{3}{2}x+x^2 +\frac{1}{2}x^3+O(x^4) (x\rightarrow 0)$

$G_(x)\sim 3x^2+\frac{5}{2}x-\frac{3}{2}x+o(1) (x\rightarrow 0)$

これを用いて、特異点を取り入れた2点パデ近似 $F_*(x)$ は、

$F_*(x)=\frac{2}{x+1}+\frac{2}{x+1}G(x)$

$=\frac{2}{x+1}(3x^2+\frac{5}{2}x-\frac{1}{2} +\frac{48-47x}{36x^2-10x+32} )$

となる。この関数は次の漸近展開を持つ。

$F_*(x)\sim 2+x+x^2+O(x^3) (x\rightarrow 0)$

$F_*(x)\sim 6x-1 +o(1) (x\rightarrow \infty)$

ここで、注意しなければいけないのは、

$lim_{x\rightarrow -1} F_*(x)\frac{x+1}{2}=\frac{95}{78}$

となり特異点の振る舞いを完全には取り入れきれないことである。ただ、 $x=-1$ で係数 $2$ に近い値で発散することのみ記述されている。

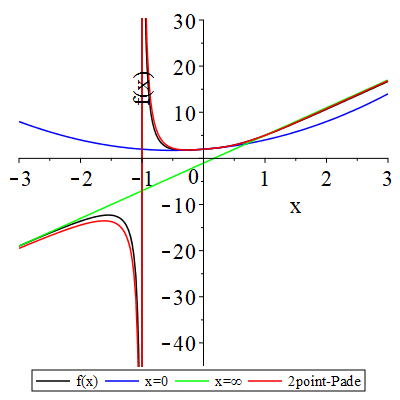
それでは、特異点を取り入れた2点パデ近似をプロットしたものを見てみよう。

f:id:FoxQ:20200721172048p:plain

今回は、 $x=-1$ 以外の特異点がたまたま存在せず、特異点を取り入れた2点パデ近似が非常によい近似となっていることがわかる。

*1:有理数の場合も変数変換を用いれば同様の解析が可能である。

*2:特異点も入れているので、3点パデ近似と呼んでもいいかもしれない。