対数関数を多項式で近似したときの零点の話【無限乗積展開!?】

対数関数のテイラー展開と多項式近似

　前回の記事で指数関数を多項式で近似した場合に零点がどのように分布するのかについて調べた。

sky-time-math.hatenablog.jp

　指数関数を調べたついでに対数関数の場合も調べてみようと思ったので、やってみた、というのが今回のお話です。*1
　ついでとは言ったが、対数関数 $\log (1+x)$ が指数関数とでは、 $x=-1$ で負の無限大に発散するという決定的に異なる点がある。そのため、「このことが多項式近似の零点分布にどのような影響を及ぼすのだろうか？」という疑問もモチベーションになっている。

　さて、対数関数は、次の形でのテイラー展開ができる。

$\log (1+x) = - \sum_{n=1}^{\infty} \frac{(-1)^n}{n}x^n$ ……(1)

$x=0$ が零点であることは自明なので、両辺を $x$ で割って、 $\log (1+x)$ を多項式で近似した場合の非自明な零点を調べたい。つまり、次の多項式で近似したときの零点を調べる。

$\frac{\log (1+x)}{x} \simeq \sum_{n=0}^{N} \frac{(-1)^n}{n+1} x^n$ ……(2)

　プログラムは前回の指数関数の多項式近似の零点を調べたときと、同様のものを使用した。つまり、多項式(2)の零点をnumpy.rootsで計算した。また、計算の精度を確認するため、計算した零点を持つ多項式を復元し、元の多項式と比較して、係数の最大値と最小値が十分小さいことをチェックしてある。

零点の分布

まずは、多項式(2)の次数 $N$ が小さいところから見ていこう。 $N=4,6,8,10$ の場合は次のようになる。

f:id:FoxQ:20181006100849p:plain

f:id:FoxQ:20181006100857p:plain

f:id:FoxQ:20181006100906p:plain

f:id:FoxQ:20181006100913p:plain

　なんとなく円形にならんでいるように見える。ここからは、一気に次数を増やしてみてる。 $N=20,50,70,100$ の場合は、次のようになる。*2

f:id:FoxQ:20181006100928p:plain

f:id:FoxQ:20181006100935p:plain

f:id:FoxQ:20181006100947p:plain

f:id:FoxQ:20181006100958p:plain

　次数を増やしていくと、思いっきり円形に並んでいることがわかった。また、次数を増やしていくと円(楕円?)の半径が1に近づいていくことも分かった。

零点の絶対値の最大・最小

　指数関数の場合と同様に、零点の絶対値の最大値と最小値も調べてみた。
　まず、次数 $N=1 \sim 15$ までを見てみる。赤線が零点の絶対値の最大値で、青線が最小値だ。

f:id:FoxQ:20181006101347p:plain

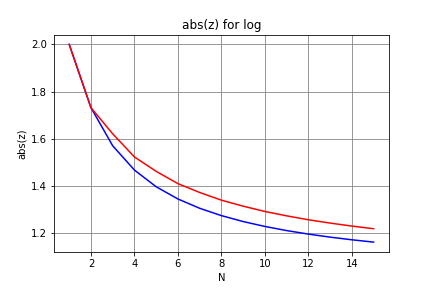
次数が増えるにつれて、円(楕円?)の半径が単調に減少にしていることがわかる。次に、 $N=100$ までを見てみる。

f:id:FoxQ:20181006101613p:plain

　次数が十分大きくなると、零点の分布が半径1の円に漸近していっているように見える。おそらく、 $N \rightarrow \infty$ の極限をとると半径1の円になるのだろう。半径が1になっている理由は、 $\log (1+x)$ が $x=-1$ で $- \infty$ に発散することに関係しているためかと思われる。
　これらの零点が $N \rightarrow \infty$ の極限で元の対数関数と何らかの関係を持ち得るか？という素朴な疑問が上がってくる。率直に考えるなら、

$\log(1+x) = x \prod_{x_0 \in \Gamma} (1-\frac{x}{x_0})$ ……(3)

という無限乗積展開のようなものがあるようにも思えてくる。ここで、 $x_0$ は半径1の円上の点で、 $\Gamma$ は半径1の円のなんらかの部分集合である*3。
　しかしながら、対数関数 $\log (1+x)$ の零点は $x=0$ のみであるはずなので、このような無限乗積展開に意味を与えるのはどうにも難しそうである。
　さて、今回はここまでです。みなさんはどう考えますか？